Negli ultimi anni si è sempre sentito più parlare della sequenza di Fibonacci grazie al suo utilizzo in ambito cinematografico e letterario (Il Codice Da Vinci).
Ma Chi era Fibonacci?
Leonardo Pisano, detto Fibonacci perché “figlio (filius) del Bonacci” nacque a Pisa nel 1170 e morì sempre nella sua Pisa nel 1240. Egli fu Matematico in un epoca in cui le scienze erano di pochi eletti e sotto controllo ecclesiastico al punto che si era perso molto del sapere matematico precedente durante il Medioevo e l’ultima parte dell’età classica.
Dobbiamo a lui l’introduzione dei numeri arabi in Europa poiché dopo la sua morte lasciò come testamento la pubblicazione di un libro, “Liber abbaci” in cui nel primo capitolo venivano introdotte le 9 cifre che tutti conosciamo più lo zero. Nei capitoli successivi di questo libro descrisse anche alcuni calcoli radicali ed introdusse la barra delle divisioni, conosciuta nel mondo arabo da molto tempo, ma con poco successo in Europa.
Per rendere le cifre arabe più comprensibili introdusse anche una tabella comparativa tra cifre arabe e romane poiché ai tempi si utilizzavano i numeri romani ed il sistema di numerazione greco mentre per fare i calcoli si usava l’abaco.
Queste novità, che avrebbero semplificato di molto la vita dei commercianti e di tutti coloro che avevano a che fare quotidianamente con i numeri, non vennero molto accettate in Europa ed in Italia al punto che nel 1280 Firenze proibì l’utilizzo della numerazione araba ai banchieri . Si riteneva lo zero come fuorviante e capace solamente di generare confusione; inoltre si pensava, che lo zero venisse utilizzato per creare messaggi segreti.
L’uso delle cifre arabe rimase quindi uso di pochi colti ma anche in precedenza qualche dotto dell’epoca era a conoscenza di queste cifre arabe; si ha infatti notizia di tale monaco Gerberto (che divento Papa come Silvestro II) il quale propose il sistema arabo in alcuni conventi dove si studiavano le scienze e si scrivevano tali opere, ma l’utilizzo rimase circoscritto in questi luoghi e tenuto quasi segreto al mondo esterno.
Ma che cosa è la serie di Fibonacci?
La Serie di Fibonacci è una sequenza numerica, formata da numeri interi naturali, la cui caratteristica principale è che ogni numero nuovo della serie si ottiene dalla somma dei due numeri che lo precedono.
Matematicamente parlando possiamo definire i primi due termini della serie come:
F0:= 0 ed F1:= 1 e chiedendo che per ogni successivo sia Fn := Fn-1 + Fn-2 con n>1
Otteniamo così, ad esempio:
0 (F0), 1 (F1) 1, 2, 3, 5, 8, 13, 21, 34, 55…
NB: La serie di Fibonacci in realtà non è solo una, più correttamente dovremmo parlare "delle" serie di Fibonacci, poiché la base di partenza può essere una coppia di numeri qualsiasi.
E' infatti una serie di Fibonacci, qualsiasi successione numerica che si comporti nel modo seguente:
a+b=c
b+c=d
c+d=e
d+e=f
Proprietà:
1) La proprietà più conosciuta di queste serie è sicuramente lo stretto legame che la lega al numero algebrico irrazionale detto sezione aurea (o numero di Fidia). Ricordiamo che la sezione, o rapporto, aureo ha un valore approssimato di 1,6180. Nella serie di Fibonacci il rapporto tra un numero della serie ed il suo predecessore dà approssimativamente il rapporto aureo e la precisione di approssimazione a questo rapporto aureo aumenta col proseguire lungo la successione di Fibonacci (Fn)
ES: 55/34= 1.6176… approssimato a 1.618 (rapporto aureo!)
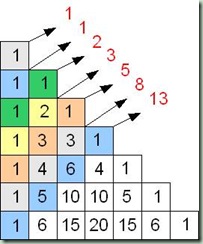
2) Altra proprietà molto conosciuta è sicuramente l’affinità tra la serie di Fibonacci e il triangolo di Tartaglia.
Come da immagine si può notare come la somma delle diagonali formi la serie di Fibonacci.
Per altre proprietà rimando a libri di testo di matematica (Es: Zwirner- Istituzioni di matematica) oppure ad internet (Wikipedia, forum di matematica ecc…).
Legami dei numeri di Fibonacci con altri settori
Come abbiamo visto i numeri di Fibonacci sono legati, in ambito matematico, al rapporto aureo, ma anche ai frattali, alle frazioni continue ecc ecc…
FISICA: Vi è legame tra numeri di Fibonacci e teoria delle stringhe. Si può affermare con certezza che a determinare il numero D di dimensioni in cui le stringhe possono vibrare sono chiaramente i numeri F di Fibonacci, in base alla formula D = 2F, con F da 1 a 13, che ci danno i numeri di dimensioni coinvolte nelle teorie delle stringhe: 2, 4, 6, 10, 16, 26.
Chimica: In chimica sono state trovate correlazioni tra la sezione aurea e Fibonacci a livello strutturale quantistico critico di alcune sostanze.
Botanica: In botanica quasi tutti i fiori hanno 3 o 5 o 8 o 13 o 21 o 34 o 55 petali. Ed anche il verso delle infiorescenze di altri fiori formano spirali che possono essere ricondotte ai numeri di Fibonacci. Tuttavia, alcuni studi identificano questa tendenza a spirale non veramente una serie di Fibonacci poiché sembra che la spirale che spesso si trova in natura (anche nel mondo animale) non sia riconducibile ad una serie di Fibonacci per numeri elevati della “spirale creata da madre natura”
Anatomia umana: Vi è rapporto aureo fra braccio e avambraccio e tra la lunghezza delle falangi del dito medio e anulare di un uomo adulto.
Musica: Le serie di Fibonacci si possono utilizzare per far musica in quanto la musica ha una forte componente matematica (durata temporale di un brano, numero di note o di battute..ecc.ecc). Questa convinzione però spesso si è rivelata forviante, ricercando la successione di Fibonacci anche dove essa non c’era. Esistono però molti musicistim tra cui i famosi Genesis, che utilizzavano volontariamente la sequenza di Fibonacci nella costruzione armonico-temporale dei loro brani; ad esempio Firth of Fifth. Esistono molti altri gruppi che hanno fatto uso di Fibonacci per le loro composizioni musicali; fra questi i Deep Purple nel brano Child in Time e i Dream Theater nell'album Octavarium, interamente concepito secondo il rapporto tra i numeri 8 e 5 e termini consecutivi della sequenza di Fibonacci. Risale invece al 2001 Lateralus album della band americana Tool che contiene il singolo omonimo "Lateralus" costruito fedelmente sulla serie di Fibonacci.
Arte: L’artista Mario Merz ha utilizzato questa successione per creare una installazione luminosa sulla Mole Antonelliana a Torino. E molte altre installazioni a tema sono presenti nel mondo fatte da Merz e da altri artisti. Si trovano rapporti aurei e successioni di Fibonacci anche in monumenti dell’antichità come le piramidi, il Partenone, nella Gioconda e nella Venere di Botticelli (questi ultimi attraverso, ad esempio, son riconducibili ai rettangoli aurei, i quali possono essere costruiti seguendo le successioni di Fibonacci).
Telefilm: Serie televisive come Lost (venne inserite una serie numerica ispirata a Fibonacci chiamata equazione di Valenzetti), Fringe (in alcune puntate è presente la successione nel laboratorio di Bishop oppure lui stesso la enuncia) e Touch (i numeri di Fibonacci sono scritti in un quaderno del ragazzino protagonista della serie) hanno tutte dedicato puntate a questa successione.
Concludo questo mio excursus sul “serie magica” di Fibonacci inserendo uno spezzone di un film italiano, di Davide Ferraio, dal titolo “Dopo Mezzanotte”. Guardatelo…. Capirete perché l’ho inserito. ;)
https://www.youtube.com/watch?v=PDIDny66SnY

Nessun commento:
Posta un commento